寿命
直线运动系统的寿命 当直线运动系统受到负荷后进行直线往复运动时,滚动体或轨道面会不断受到反复应力的作用,因此,如果直线运动长时间持续...
直线运动系统的寿命
当直线运动系统受到负荷后进行直线往复运动时,滚动体或轨道面会不断受到反复应力的作用,因此,如果直线运动长时间持续时,就会出现由于材料的疲劳而导致的被称为剥落的鱼鳞状的损坏情况。第一次出现该剥落前的总移动距离被称为直线运动系统的寿命。此外还可能存在由于烧结、破裂、啃咬、生锈等原因而使直线运动系统不能使用的情况,但是这些主要属于安装精度、环境、润滑方法等方面的问题,应与寿命区别对待。
额定寿命
由于直线运动系统具有如下性质: 即使同时制作的相同公称型号的产品在相同条件下运转,材料的疲劳损坏不一致的情况比较多,因此,直线运动系统本身的寿命也可能会不一致,个别直线运动系统很难正确预测寿命。因此,一般在预测寿命时使用综合规定的额定寿命。额定寿命的定义如下:“一组相同的直线运动系统在同一条件下分别行驶时,其中90%的直线运动系统不会出现剥落,而可以顺利到达的移动距离。”
基本动额定负荷(以ISO14728-1为准※2)与基本动额定扭矩
由于直线运动系统的额定寿命由移动距离表示,因此,移动距离设为恒定值时的负荷作为直线运动系统的负载能力使用于寿命的计算中。该负荷被称为基本动额定负荷,定义为“可得到50×103m的额定寿命的大小和方向均为恒定值的负荷”。根据直线运动系统类型的不同,各负荷方向的负载能力可能有所不同,因此,为了方便起见,NB将直线运动系统正上方施加负荷时的额定负荷记载于尺寸表中。关于滚珠花键,可能会受到扭矩负载而进行直线运动,因此,同样规定了基本动额定扭矩。
※2 部分产品中有不适用的情况。
额定寿命的预测
 寿命计算式会由于直线运动系统中使用的滚动体的种类的不同而异,使用钢球时为方程式(3),使用滚柱时为方程式(4)。另外,当直线运动系统承受扭矩负载时使用方程式(5)。
寿命计算式会由于直线运动系统中使用的滚动体的种类的不同而异,使用钢球时为方程式(3),使用滚柱时为方程式(4)。另外,当直线运动系统承受扭矩负载时使用方程式(5)。

实际使用直线运动系统时,会受到导向轴的精度、安装状态、使用环境、运动中的振动或冲击等各种不确定要素的影响,因此很难算出正确的作用负荷。一般将这些要素作为系数使用,使寿命计算变得较为简单化,会使用硬度系数(fH)·温度系数(fT)·接触系数(fC)·负荷系数(fW)。受这些因素的影响,方程式(3)~(5)变为方程式(6)~(8)。
 如果单位时间的移动距离明确时,寿命通过时间来表示会更简单易懂。
如果单位时间的移动距离明确时,寿命通过时间来表示会更简单易懂。
行程与往复次数及寿命时间的关系如方程式(9)所示。
硬度系数(fH)
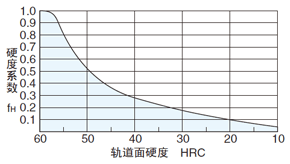
在直线运动系统中,导向轴具有与滚珠轴承的内轮相同的作用,因此,导向轴的硬度在额定负荷的决定方面是重要因素之一。如果表面硬度低于58HRC时,额定负荷也会降低。虽然在一般情况下,NB产品可借助高度的淬火技术总是保持适当的值,但在不得已的情况下,必须使用未达到适当的表面硬度的导向轴时,请使用图1-2的硬度系数补正额定负荷。
温度系数(fT)

由于在直线运动系统中实施了淬火技术,从而提高了硬度、并降低了磨损,因此,当直线运动系统的温度超过100℃时就会出现硬度降低及额定负荷降低的情况。直线运动系统的温度变化导致的硬度变化作为温度系数如图1-3所示。
接触系数(fC)

当一起使用两个以上的直线运动系统时,必须考虑各产品的不一致性和安装面加工精度的影响。一般使用表1-2的接触系数来计算寿命。
负荷系数(fW)
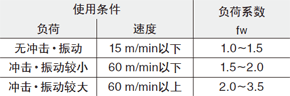
计算作用于直线运动系统的负荷时,除了物体的重量外,还需要正确计算出影响运动速度的惯性力、力矩以及各自的时间性变化。但是,由于在直线往复运动中,往往会伴随有反复的启动、停止以及振动、冲击等不确定性因素,因此很难正确地计算出负荷。一般使用表1-3的负荷系数来简化寿命的计算。
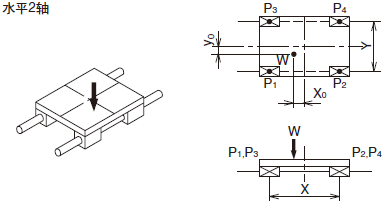
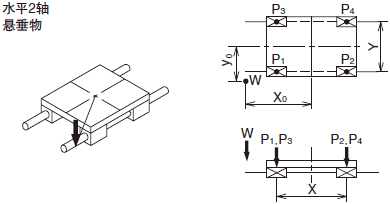
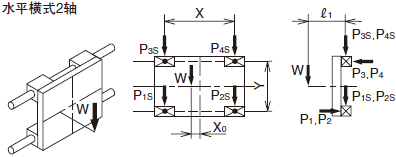
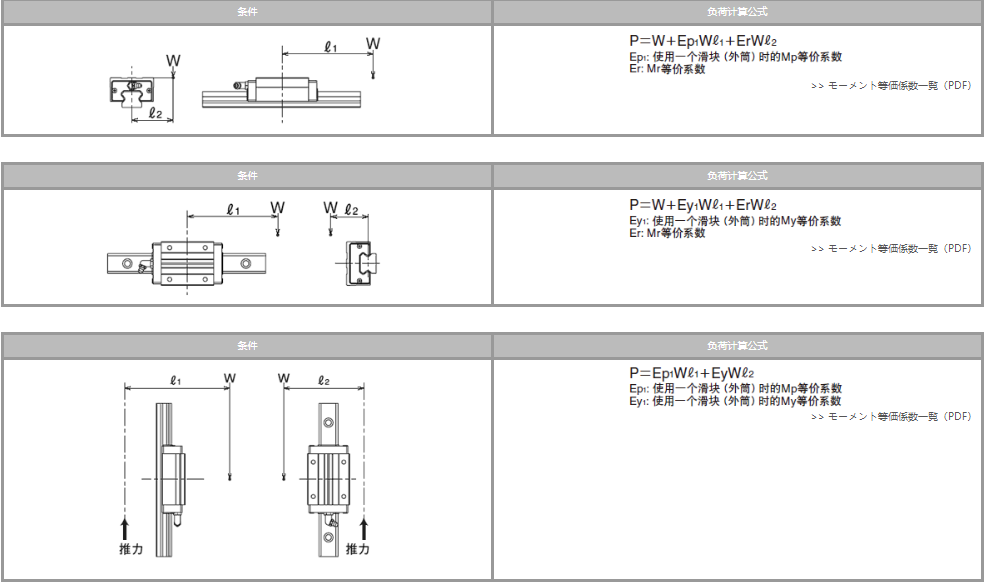
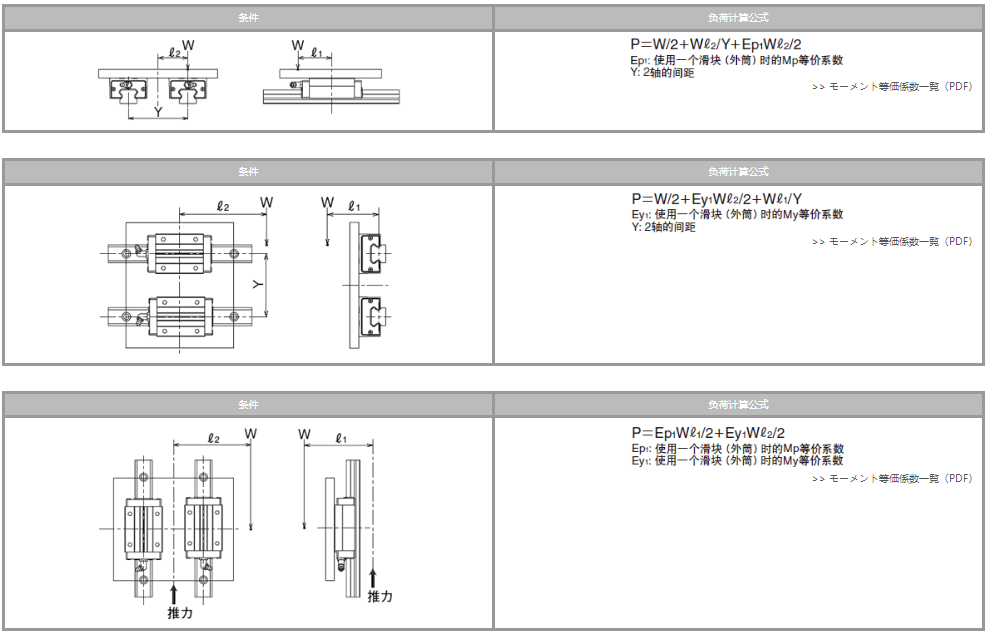
负荷的计算方法(1)
直线运动系统代表性的使用方法和直线运动系统承受的负荷的计算式如表1-4~5所示。
W: 作用负荷(N) P1~P4: 直线运动系统承受的负荷(N) X,Y: 直线运动系统的间距(mm)
x,y,![]() :至负荷作用点或工件重心的距离(mm) g:重力加速度9.8×103mm/sec2)
:至负荷作用点或工件重心的距离(mm) g:重力加速度9.8×103mm/sec2)
V:移动速度(mm/sec) t1:加速时间(sec) t3:减速时间(sec)
静止または等速運動時
条件 | 负荷计算公式 |
 |
条件 | 负荷计算公式 |
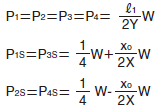 |
条件 | 负荷计算公式 |
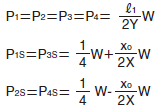 |
条件 | 负荷计算公式 |
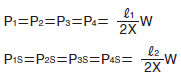 |
等加速度運動時
条件 | 负荷计算公式 |
 |
等价系数
 |
直线运动系统的使用方法是1轴使用多个滑块(外筒),虽然一般也会使用2轴,但由于安装空间等问题,有时也会在1轴上使用一个或紧靠使用两个以上的滑块(外筒)。此时,计算负荷时请给作用力矩负载乘以表1-7~25所示的力矩等价系数。力矩作用于直线运动系统时的等价负荷的计算式如下所示。
负荷的计算方法(2)
リニアシステムにモーメントが作用した場合の荷重計算式を下表に示します。
W:作用负荷(N) P:直线运动系统承受的负荷(N) ![]() :至滑块(外筒)中心的距离(mm)
:至滑块(外筒)中心的距离(mm)
1軸使用
2軸使用
变动负荷的平均负荷
一般来说,根据使用方法的不同,作用于直线运动系统的负荷可能会有各种变化。例如,往复运动的启动、停止定速运动,或工件的有无等。这样,对于变动负荷来说,就有必要求出实现与该条件下的寿命相等的寿命的平均负荷,从而进行寿命计算。
根据距离的不同负荷发生阶段性变化的情况时
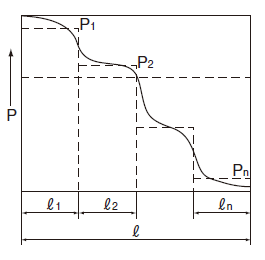
承受负荷P1的移动距离 ![]() 1
1
承受负荷P2的移动距离 ![]() 2・・・・・
2・・・・・
▼
承受负荷Pn的移动距离 ![]() n的情况
n的情况
平均负荷Pm根据以下方程式求出。
负荷基本为直线性变化时(图1-8)
平均负荷Pm的近似值可根据以下方程式求出。
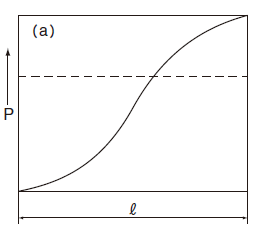
负荷如图1-9(a)·(b)发生正弦曲线的变化时
可根据以下方程式求出平均负荷Pm的近似值。
更多详情请咨询上海寅威精密机械有限公司 电话:021-66696985 15000451640